Las Ecuaciones en Derivadas Parciales (EDP) son aquellas ecuaciones que involucran las derivadas parciales de una función desconocida con dos o más variables independientes. Su estudio se inicia en el siglo XVIII con los trabajos de los suizos d’Alembert y Euler, y los franceses Lagrange y Laplace, los cuales surgieron en el contexto de la modelización matemática de fenómenos de la física del medio continuo.

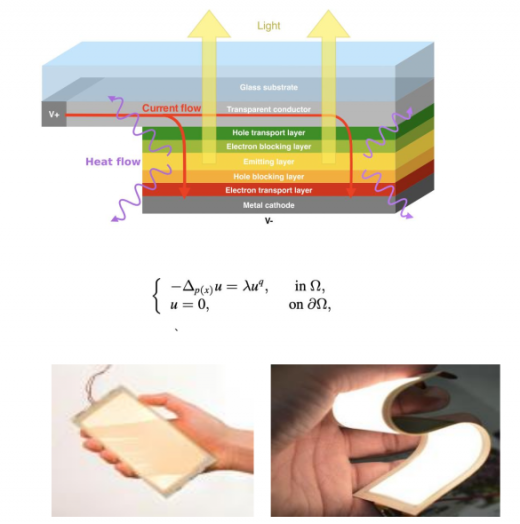
En esta tesis se estudia la existencia, unicidad y regularidad de soluciones de EDP que provienen del estudio de diferentes campos como son la dinámica de poblaciones, el flujo de corriente de las pantallas OLED, las estructuras estelares, la rugosidad de superficies o la teoría de Thomas-Fermi que describe la interacción de los núcleos de átomos.

- J. Carmona, A. Molino y J. Rossi: “The Gelfand Problem for the 1-homogeneous p-Laplacian”, Advances in Nonlinear Analisys (2017). https://doi.org/10.1515/anona-2016-0233

- D. Arcoya, A. Molino y L. Moreno-Mérida: “Existence and Regularizing Effect on Degenerate Lower Order Terms in Elliptic Equations Beyond the Hardy Constant”, Advances Nonlinear Studies (2018). https://doi.org/10.1515/ans-2018-0003

- T. Leonori, A. Molino y S. Segura de León: “Parabolic Equations with natural growth approximated by nonlocal equations”. Communications in Contemporary Mathematics (2021). https://doi.org/10.1142/S0219199719500883